Asymmetric Algorithms

Berdasarkan postingan sebelumnya tentang algoritnma yang digunakan.. Jika yang kemarin tentang Symmetric Algorithms kali ini aku akan share yang ke dua..

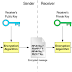
Algoritma kriptografi nirsimetris adalah algoritma yang menggunakan kunci yang berbeda untuk proses enkripsi dan dekripsinya.Algoritma ini disebut juga algoritma kunci umum (public key algorithm) karena kunci untuk enkripsi dibuat umum (public key) atau dapat diketahui oleh setiap orang, tapi kunci untuk dekripsi hanya diketahui oleh orang yang berwenang mengetahui data yang disandikan atau sering disebut kunci pribadi (private key).Contoh algoritma terkenal yang menggunakan kunci asimetris adalah RSA

a.  RSA (Rivest-Shamir-Adleman)

Algoritma RSA diperkenalkan oleh tiga orang peneliti dari MIT (Massachussets Institute of Technology), yaitu Ron Rivest, Adi Shamir, dan Len Adleman, pada        tahun 1976. RSA mendasarkan proses enkripsi dan deskripsinya pada konsep bilangan prima dan aritmatika modulo.Baik kunci enkripsi maupun kunci deskripsi keduanya merupakan bilangan bulat.Kunci enkripsi tidak dirahasiakan dan diketahui umum (sehingga dinamakan juga kunci publik), namun kunci untuk deskripsi bersifat rahasia.Kunci deskripsi dibangkitkan oleh beberapa buah bilangan prima bersama-sama dengan kunci enkripsi. Untuk menemukan kunci enkripsiseseorang harus memfaktorkan suatu bilangan non proma menjadi faktor primanya Kenyataannya, memfaktorkan bilangan non-prima menjadi faktor primanya bukanlah pekerjaan yang mudah.Belum ada algoritma yang efisien yang ditemukan untuk pemfaktoran itu. Semakin besar bilangan non-primanya tentu akan semakin sulit menemukan faktor primanya.Semakin sulit pemfaktorannya, semakin kuat pula algoritma RSA.Algoritma RSA sebenarnya sederhana sekali.Secara ringkas, algoritma RSA adalah sebagai berikut.

Kekuatan dan Keamanan RSA

            Kekuatan RSA terletak pada tingkat kesulitan menjadi faktor primanya, yang dalam hal ini n = a × b. Sekali n berhasil difaktorkan menjadi a dan b maka m = (a – 1) × (b – 1) dapat dihitung.Selanjutnya, karena kunci enkripsi e diumumkan (tidak rahasia), maka kunci deskripsi d dapat dihitung dari persamaan e × d ≡ 1 (mod m). Ini berarti proses deskripsi dapat dilakukan oleh orang yang tidak berhak.Penemu algortima RSA menyarankan nilai a dan b yang dipakai panjangnya lebih dari 100 digit,berukuran lebih  dari  200 digit.Bayangkan berapa besar usaha kerja yang diperlukan untuk memfaktorkan bilangan bulat 200 digit menjadi faktor primanya. Menurut Rivest dan kawan- kawan, usaha untuk mencari faktor bilangan 200 digit membutuhkan waktu komputasi selama 4 milyar tahun.(Dengan asumsi bahwa algoritma pemfaktoran yang digunakan adalah algoritma tercepat saat ini dan komputer yang dipakai mempunyai kecepatan 1 milidetik).Untunglah algoritma yang paling mangkus untuk memfaktorkan bilangan yang besar belum ditemukan.Inilah yang membuat algoritma RSA tetap dipakai hingga saat ini.Selagi belum ditemukan algoritma yang mangkus untuk memfaktorkan bilangan bulat menjadi faktor primanya, maka algoritma RSA masih direkomendasikan untuk penyandian pesan.


semua ada di sini